Oblig 8: Optimering og løsing av likninger#
Læringsmål
I dissse oppgavene skal du lære og vise at du behersker følgende:
Bruke numerisk derivasjon til å analysere eksperimentelle data.
Finne ekstremalpunkter vha. numerisk derivasjon, og tolke resultatene.
Forklare og implementere Newtons metode som en funksjon med relevant feilhåndtering.
Bruke Newtons metode for å finne nullpunkter og løse likninger.
Titrering#
Titrering er en kvantitativ analysemetode der vi bestemmer konsentrasjonen av et ukjent stoff (analytten) ved å tilsette et stoff med kjent konsentrasjon (titranten). Titranten tilsettes ofte fra en byrette, og vi kan notere oss pH i analytten underveis ettersom vi tilsetter et visst volum titrant. Her er en titreringskurve for titrering av en svak syre med en sterk base.
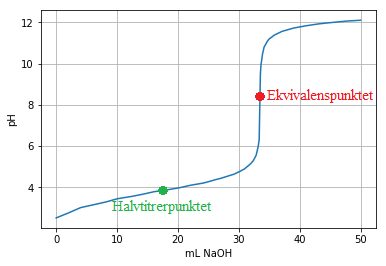
Ved ekvivalenspunktet er grafen brattest, og her er stoffmengdene av syre og base ekvivalente (og dermed like hvis forholdet er 1:1 i reaksjonslikningen). Dette kan vi bruke til å finne konsentrasjonen av analytten. Ved halvtitrerpunktet er \(pH = pK_a\), og vi har en bufferløsning. Derfor endrer pH-en seg ikke så mye rundt dette punktet. Vi skal se på noen metoder for å finne ekvivalenspunktet og pH-en ved ekvivalenspunktet i en slik titrering.
pH ved ekvivalenspunktet#
Vi kan utlede likninger som gir oss pH-en ved tilsetting av et visst volum syre til base, eller motsatt. Når vi titrerer, tilsette vi sterke syrer til baser eller sterke baser til syrer. Derfor konsenterer vi oss om å utlede likninger som kan beskrive pH-en i slike løsninger. Vi tar utgangspunkt i en generell syre-base-titrering der vi titrerer en svak syre (HA) med en sterk base (BOH):
Etter at en slik titrering er fullført, kjenner vi til følgende:
Konsentrasjonen av basen vi brukte (titranten): \(c_b\).
Volumet base vi brukte for å nå ekvivalenspunktet: \(V_b\).
Volumet syre vi titrerte (analytten): \(V_a\).
Den tidligere ukjente konsentrasjonen av syra: \(c_a\).
Siden vi kjenner disse verdiene, er de å regne som konstanter når vi skal finne pH i løsningen ved ekvivalenspunktet. Vi trenger å formulere en likning som inneholder \([H^+]\), og ingen andre ukjente. La oss prøve å utlede en slik likning. Et godt utgangspunkt kan være at summen av negative ioner til enhver tid skal være lik summen av positive ioner, siden løsningen alltid er elektrisk nøytral:
\begin{equation} \label{eqn:elektronoytralitet} [H^+] + [B^+] = [OH^-] + [A^-] \end{equation}
Denne sammenhengen kan vi ta utgangspunkt i, men vi trenger å eliminere alle de ukjente konsentrasjonene bortsett fra \([H^+]\), som vi jo skal finne. Merk at \([B^+]\) og \([A^-]\) er konsentrasjonen i løsningen etter tilsatt titrant, mens \(c_b\) og \(c_a\) er konsentrasjon av base i titranten og syre i analytten \textit{før} titreringen starter (initialbetingelser).
Konsentrasjonen av den korresponderende syra, \([B^+]\), til den sterke basen i \textit{løsningen} ved enhver tid er gitt ved antallet mol base tilsatt delt på totalvolumet av løsningen. Dette er fordi vi regner med at all basen vi tilsetter, har reagert. Antall mol base tilsatt er det samme som konsentrasjonen av basen ved start (\(c_b\)) multiplisert med volumet av base som er tilsatt. Deretter får vi konsentrasjonen av base i løsningen ved å dele på totalvolumet av løsningen, \(V_t = V_a + V_b\). Da får vi at:
\begin{equation} \label{eqn:korrsyre} [B^+] = \frac{c_bV_b}{V_t} \end{equation}
Da har vi altså fått et uttrykk for konsentrasjonen til den sterke basen, som vi kan sette inn i likningen for elektronnøytralitet. Vi mangler da blant annet et uttrykk for \([OH^-]\). Dette kan vi få fra uttrykket for vannets egenprotolyse:
\begin{equation} \label{eqn:egenprotolyse} K_w = [OH^-][H^+] \end{equation}
der \(k_w = 10^{-14}\). Da har vi nok et uttrykk som vi kan sette inn i likningen for elektronnøytralitet:
\begin{equation} \label{eqn:hydroksid} [OH^-] = \frac{K_w}{[H^+]} \end{equation}
Vi mangler nå et uttrykk for \([A^-]\). Vi kan utlede dette fra følgende sammenheng:
\begin{equation} \label{eqn:syrelikevekt} n_{A^-} = n_{syre,start} - n_{HA} \end{equation}
Denne sammenhengen sier at antall mol korresponderende base til en svak syre er lik antall mol syre vi startet med minus antall mol syre vi har igjen. Dette gir igjen følgende sammenheng:
\begin{equation} \label{eqn:syrelikevekt2} [A^-]\cdot V_t = c_aV_a - [HA]\cdot V_t \end{equation}
Et problem er at vi nå har en ukjent til i likningen ovenfor, nemlig \([HA]\). Denne kan vi derimot eliminere ved å benytte oss av uttrykket for likevektskonstanten for en svak syre:
\begin{equation} \label{eqn:likevektskonstant1} K_a = \frac{[H^+][A^-]}{[HA]} \end{equation}
Dette gir følgende uttrykk for konsentrasjonen av syra, \([HA]\):
\begin{equation} \label{eqn:likevektskonstant2} [HA]= \frac{[H^+][A^-]}{K_a} \end{equation}
Hvis vi substituerer \([HA]\) fra dette uttrykket inn i uttrykket for \([A^-]\), får vi:
\begin{equation} \label{eqn:korrbase} [A^-] = \frac{c_aV_a}{V_t[H^+]/K_a + V_t} = \frac{c_aV_aK_a}{V_t([H^+]+K_a)} \end{equation}
Nå har vi uttrykk for \([A^-]\), \([OH^-]\) og \([B^+]\) som kun avhenger av én ukjent, nemlig \([H^+]\). Da kan vi sette alt inn i likningen for elektronnøytralitet:
\begin{equation} \label{eqn:syrebaselikning1} [H^+] + \frac{c_bV_b}{V_t} = \frac{K_w}{[H^+]} + \frac{c_aV_aK_a}{V_t([H^+]+K_a)} \end{equation}
Vi samler alle ledd på samme side og ganger alle ledd med \(V_t\) for å fjerne flest mulige brøker:
\begin{equation} \label{eqn:syrebaselikning2} [H^+]V_t + c_bV_b - \frac{K_wV_t}{[H^+]} - \frac{c_aV_aK_a}{[H^+]+K_a} = 0 \end{equation}
Nå har vi en likning som vi kan løse ved å finne nullpunktene til følgende funksjon:
\begin{equation} \label{eqn:syrebasefunksjon1} T([H^+]) = [H^+]V_t + c_bV_b - \frac{K_wV_t}{[H^+]} - \frac{c_aV_aK_a}{[H^+]+K_a} \end{equation}
Denne funksjonen er det derimot problematisk å finne nullpunktene til. Vi får nemlig asymptoter rundt nullpunktet fordi den ikke er definert når \([H^+] = 0\). Dette kan vi komme unna ved å gange med fellesnevner, \([H^+]\cdot(K_a + [H^+])\), i alle ledd. Da får vi følgende funksjon:
\begin{equation} \label{eqn:syrebasefunksjon2} T([H^+]) = V_t([H^+] + K_a)[H^+]^2 + c_bV_b([H^+] + K_a)[H^+] - K_wV_t([H^+] + K_a) - c_aV_aK_a[H^+] \end{equation}
Vi ser at dette er en tredjegradsfunksjon som ikke så lett lar seg løses analytisk (selv om det er mulig!). Vi kan derfor bruke numeriske løsninger, for eksempel Newtons metode, for å løse denne.
Merk at likningen funksjonen ikke har noen fysisk eller kjemisk betydning, men et av nullpunktene til funksjonen gir pH-en i en blanding der sterk base er tilsatt svak syre.
8.1 Beregning av ekvivalenspunktet#
a) Les og plott dataene fra fila titreringsdata.txt, som viser titreringsdata for titrering av glykolsyre med NaOH. Sørg for at datapunktene vises i plottet.
b) Deriver pH-en numerisk med hensyn på volumet og legg den deriverte pH-en i ei ny liste. Forklar hva den deriverte av pH-en kan fortelle oss.
c) Lag en funksjon som finner den største deriverte i den deriverte lista. Sammenlikn gjerne med numpy-funksjonen max. La programmet skrive ut hvilket volum dette tilsvarer. Dette er volumet sterk base som er tilsatt ved ekvivalenspunktet. Finn også pH ved ekvivalenspunktet ved hjelp av programmet ditt.
8.2 Beregning av pH ved ekvivalenspunktet#
Titreringen er utført slik at 0.0100 L glykolsyre (\(K_a\) = \(1.50\cdot 10^{-4}\)) ble titrert med 0.500 M NaOH. Forbruket av NaOH var 33.52 mL.
a) Regn ut konsentrasjonen av syra og lag alle variablene du trenger for å kunne regne med den siste funksjonen \(T([H^+])\) i teoridelen.
b) Tilpass kodesnutten under til egen kode og regn ut pH-en ved ekvivalenspunktet. Hvordan passer dette med utregningen i oppgave a? pH-en skal bli 8.70. Kommenter resultatet.
# Utregna pH-verdi ved ekvivalenspunktet
Kb = 6.67E-11
V_total = (V_NaOH + V_glykolsyre)
c_glykolsyre_ekv = n_glykolsyre/V_total
c_OH = np.sqrt(Kb*c_glykolsyre_ekv)
pOH = -np.log10(c_OH)
pH = 14-pOH
print(f'pH ved ekvivalenspunktet er {pH}')
c) Lag en Python-funksjon av funksjonen i \(T([H^+])\). Plott funksjonen i intervallet \([-1,1]\). Hva ser du? Prøv å plotte i intervallet \([-1\cdot10^{-8}, 1\cdot10^{-8}]\). Hvordan ser det ut nå? Negativ konsentrasjon gir ingen mening reint kjemisk, men vi bruker det som en teoretisk størrelse for å finne nullpunktene til funksjonen vår.
d) Forklar hvordan Newtons metode fungerer.
e) Lag en funksjon som benytter Newtons metode til å finne nullpunktene til \(T([H^+])\). Begrunn valget av startpunktet a.
f) Beregn pH-en ut fra det du fikk i forrige oppgave. Kommenter eventuelle avvik eller likheter med de andre beregningene.
