Forelesning 9: Reaksjonskinetikk II

\[A \rightarrow B\]

\[\frac{d[B]}{dt} = k[A]\]

import numpy as np
import matplotlib.pyplot as plt

# Initialbetingelser
k = 0.1 # Fartskonstanten
A0 = 1  # Startkonsentrasjon (mol/L)
B0 = 0  # Startkonsentrasjon (mol/L)

t0 = 0  # Starttid (s)
t_slutt = 100 # Sluttid (s)
dt = 1E-3 # Tidssteg (s)
N = int((t_slutt - t0)/dt) + 1

# Arrayer
A = np.zeros(N)
B = np.zeros(N)
t = np.zeros(N)
A[0] = A0
B[0] = B0

# Integrasjonsløkke
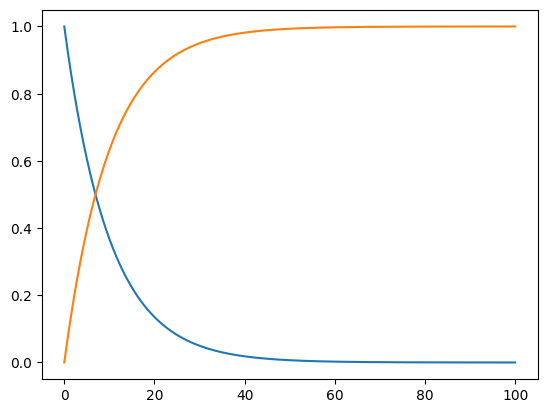
for i in range(N - 1):
    dBdt = k*A[i]**2 # Fartsloven
    dAdt = - dBdt
    # Eulers metode
    B[i+1] = B[i] + dBdt*dt
    A[i+1] = A[i] + dAdt*dt
    # Oppdatere tida
    t[i+1] = t[i] + dt

plt.plot(t, A)
plt.plot(t, B)
plt.show()

Løse ODE-er med biblioteker

from scipy.integrate import solve_ivp

def fartslover(t,y):
    # t = tidsparameteren
    # y = [HI, H2, I2], altså startbetingelser
    HI = y[0]
    H2 = y[1]
    I2 = y[2]
    k = 0.1

    dHIdt = k*H2*I2
    dH2dt = -0.5*dHIdt
    dI2dt = dH2dt

    return [dHIdt, dH2dt, dI2dt]

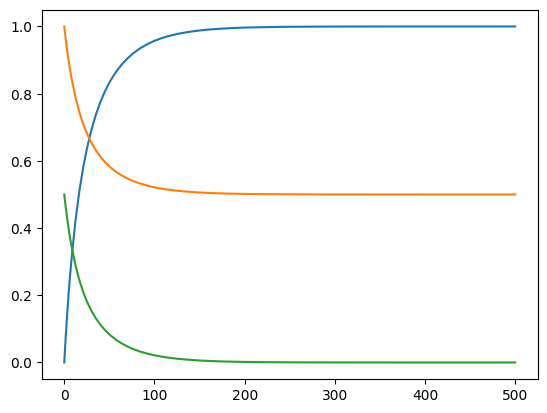
y_int = solve_ivp(fartslover, t_span = [0,500], y0 = [0, 1, 0.5], method = "BDF")
t = y_int.t
HI, H2, I2 = y_int.y

plt.plot(t,HI, t,H2, t,I2)
plt.show()