Oblig 1: Håndtering av kjemiske data#
Læringsmål
I dissse oppgavene skal du lære og vise at du behersker følgende:
Gjøre relevante statistiske beregninger.
Utføre regresjonsanalyse på eksperimentelle data, og tolke regresjonsmodellen.
Bruke numerisk derivasjon til å analysere eksperimentelle data.
Finne ekstremalpunkter vha. numerisk derivasjon, og tolke resultatene.
Analyse data ved å bruke numerisk integrasjon.
Bruke generativ KI på en produktiv måte.
1.1 Spektroskopi#
Vi bruker et datasett vi har fått fra en analyse av innholdet av \(Pb^{2+}\) i bekkevann som utgangspunkt. Til dette er det brukt spektroskopisk analyse. I spektroskopiske analyser finner vi konsentrasjonen til et stoff ved å undersøke hvor mye lys stoffet absorberer av en bestemt bølgelengde. For å finne konsentrasjonen i en ukjent løsning, lager vi først en standardkurve ut fra absorpsjonen til løsninger med kjent konsentrasjon. Vi analyserer en rekke løsninger og får følgende resultater:
Konsentrasjon (ppm) |
Absorbans |
|---|---|
0.0 |
0.0 |
0.100 |
0.116 |
0.200 |
0.216 |
0.300 |
0.310 |
0.400 |
0.425 |
0.500 |
0.520 |
Gjør denne oppgaven uten å bruke kunstig intelligens.
a) Lag et program som gjør lineær regresjon på dataene og plotter datapunktene og den tilpassede regresjonskurven i samme koordinatsystem.
b) Analysen ved 283 nm av vannprøva ga absorbans på 0.340. Bruk standardkurven og programmet til å bestemme konsentrasjonen av blyioner i vannprøva i ppm.
1.2 Gasskromatografi#
Du har fått data fra en gasskromatografi-analyse lagret i gc.csv. Filen har to kolonner: tid (retensjonstid i minutter) og signal (detektorrespons i mV).
I denne oppgaven skal du både gjøre viktig kjernearbeid selv og bruke KI som partner der det er hensiktsmessig.
a) Utforskende fase med KI som sparringspartner
Formuler en instruks (et prompt) som du kan gi til en KI for å få ideer til hvordan man kan analysere kromatografidata. Husk KROM-prinsippene.
Test instruksen med GPT-UiO (heretter referert til som “KI”). Hvilke forslag fikk du? Hvilke var passende og hvilke var ikke egnet for denne problemstillingen?
b) Prøv selv og sammenlikn med KI
Les fila med Pandas og valider at du har lest fila korrekt (dette kan gjøres på flere måter).
Få KI til å generere kode som skal lese fila. Sammenlikn med slik du har gjort det. Er det en av metodene som er best, eller var de ganske like?
Lag et enkelt plott av signal som funksjon av tid. Kopier dette programmet inn i KI og be KI om forslag til å forbedre figuren. Kjør den reviderte koden som KI foreslår.
Kommenter kort: Hva ble bedre? Var det forslag som ikke var nyttige eller som ble unødvendig kompliserte?
c) Analyse
Finn retensjonstida for den høyeste toppen uten KI.
Beregn arealet under kurven med trapesmetoden (du kan gjerne bruke scipy-funksjoner) uten bruk av KI.
Be nå KI om å finne retensjonstida for den høyeste toppen og arealet under kurven. Sammenlikn med slik du gjorde det. Hva var annerledes, og hva var likt?
d) Refleksjon Skriv kort om hvor i prosessen du mener det var viktig å gjøre jobben selv, og hvor KI var en god partner.
1.3 Titrering#
Titrering er en kvantitativ analysemetode der vi bestemmer konsentrasjonen av et ukjent stoff (analytten) ved å tilsette et stoff med kjent konsentrasjon (titranten). Titranten tilsettes ofte fra en byrette, og vi kan notere oss pH i analytten underveis ettersom vi tilsetter et visst volum titrant. Her er en titreringskurve for titrering av en svak syre med en sterk base.
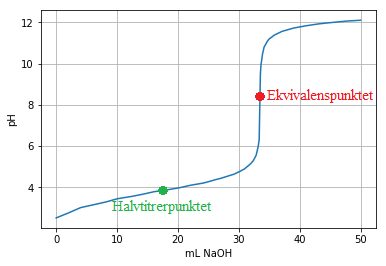
Ved ekvivalenspunktet er grafen brattest, og her er stoffmengdene av syre og base ekvivalente (og dermed like hvis forholdet er 1:1 i reaksjonslikningen). Dette kan vi bruke til å finne konsentrasjonen av analytten. Ved halvtitrerpunktet er \(pH = pK_a\), og vi har en bufferløsning. Derfor endrer pH-en seg ikke så mye rundt dette punktet. Vi skal se på noen metoder for å finne ekvivalenspunktet og pH-en ved ekvivalenspunktet i en slik titrering.
a) Les og plott dataene fra fila titreringsdata.txt, som viser titreringsdata for titrering av glykolsyre med NaOH. Sørg for at datapunktene vises i plottet.
b) Deriver pH-en numerisk med hensyn på volumet og legg den deriverte pH-en i ei ny liste. Forklar hva den deriverte av pH-en kan fortelle oss.
c) Få KI til å evaluere programmet du har laget med utgangspunkt i målet med programmet. Skriv ned og diskuter kort eventuelle endringer som KI-en foreslår.
d) Bruk KI til å lage en funksjon som finner den største deriverte i den deriverte lista, og til å bestemme pH ved ekvivalenspunktet ved hjelp av programmet ditt. Forklar med ord hvordan dette programmet fungerer. Gjør det det du ønsker at det skal gjøre?
