Forelesning 4: Statistikk II

I denne forelesningen skal vi se på statistisk inferens og hvordan vi kan bruke statistiske metoder for å trekke konklusjoner fra data.

• utføre regresjonsanalyse

• utføre og tolke hypotesetester

• regne ut og tolke korrelasjon

Repetisjon

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

df = pd.read_csv("oksygen.csv")
df.head()

	konsentrasjon_O2
0	3.2
1	3.5
2	3.3
3	5.8
4	3.1

oksygen = df["konsentrasjon_O2"]
snitt = oksygen.mean()
avvik = oksygen.std()
print(f"Oksygenkonsentrasjonen var {snitt:.1f} +- {avvik:.1f}")

Oksygenkonsentrasjonen var 4.0 +- 1.2

O2_riktig = oksygen[oksygen <= 5]
snitt = O2_riktig.mean()
avvik = O2_riktig.std()
print(f"Oksygenkonsentrasjonen var {snitt:.1f} +- {avvik:.1f}")

Oksygenkonsentrasjonen var 3.3 +- 0.2

absdata = pd.read_csv("absorbans.txt", sep = ",")
tid = absdata["tid_s"]
absorbans = absdata["abs"]

a, b = np.polyfit(tid, absorbans, 1)

x_ny = np.linspace(0, tid.max() + 0.5)
y_ny = a*x_ny + b

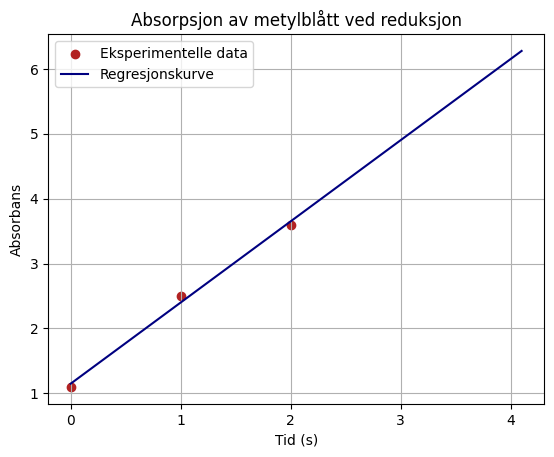
plt.scatter(tid, absorbans, color = "firebrick", label = "Eksperimentelle data")
plt.plot(x_ny, y_ny, color = "navy", label = "Regresjonskurve")
plt.xlabel("Tid (s)")
plt.ylabel("Absorbans")
plt.grid()
plt.title("Absorpsjon av metylblått ved reduksjon")
plt.legend()
plt.show()

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import linregress

# Les data
absdata = pd.read_csv("absorbans.txt", sep=",")
tid = absdata["tid_s"].to_numpy()
absorbans = absdata["abs"].to_numpy()

# Lineær regresjon (to måter; polyfit eller linregress for R^2)
a, b = np.polyfit(tid, absorbans, 1)  # a = stigning, b = intercept

# Bruk tidens spenn for x-verdiene til linjen
x_ny = np.linspace(tid.min(), tid.max(), 200)
y_ny = a * x_ny + b

# Alternativt: få R^2 og usikkerheter via scipy (valgfritt)
lr = linregress(tid, absorbans)
r2 = lr.rvalue**2

# Plot
fig, ax = plt.subplots(figsize=(7, 5))
ax.scatter(tid, absorbans, s=35, color="tab:blue", label="Målt absorbans")
ax.plot(x_ny, y_ny, color="tab:red", lw=2,
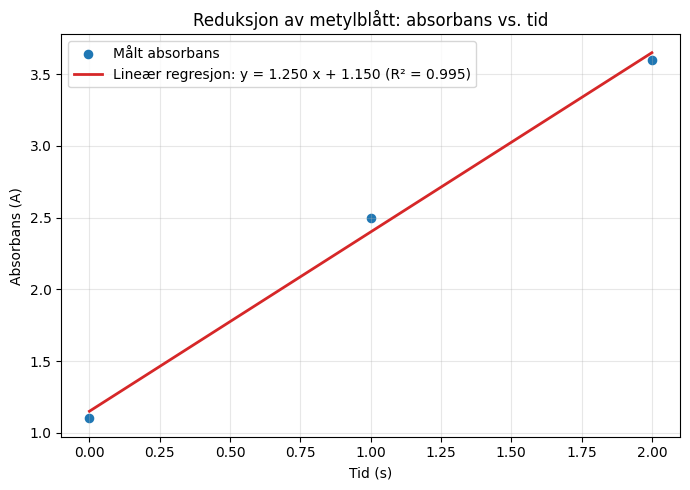
        label=f"Lineær regresjon: y = {a:.3f} x + {b:.3f} (R² = {r2:.3f})")

ax.set_title("Reduksjon av metylblått: absorbans vs. tid")
ax.set_xlabel("Tid (s)")
ax.set_ylabel("Absorbans (A)")
ax.grid(True, alpha=0.3)
ax.legend()
plt.tight_layout()
plt.show()

# Valgfritt: lagre figuren
# fig.savefig("metylblaatt_absorbans_regresjon.png", dpi=300)

Regresjon II: Curve_fit

from scipy.optimize import curve_fit

tid = np.array([0, 10, 20, 30, 40, 50 ,60])
kons = np.array([5.0, 4.3, 3.8, 3.2, 2.8, 2.4, 2.0])

def modell(x, a, b):
    return a*np.exp(-b*x)

coeff, covar = curve_fit(modell, tid, kons)
a = coeff[0]
b = coeff[1]

x_ny = np.linspace(0, tid.max() + 0.5)
y_ny = modell(x_ny, a, b)

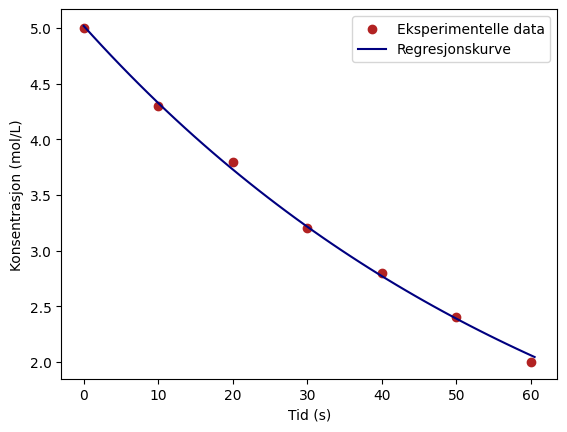
plt.scatter(tid, kons, color = "firebrick", label = "Eksperimentelle data")
plt.plot(x_ny, y_ny, color = "navy", label = "Regresjonskurve")
plt.xlabel("Tid (s)")
plt.ylabel("Konsentrasjon (mol/L)")
plt.legend()
plt.show()

/var/folders/z_/zd2_19g1205dvcvdhgk10p680000gp/T/ipykernel_9240/2671664886.py:7: RuntimeWarning: overflow encountered in exp
  return a*np.exp(-b*x)

Oppgave 1: Analyse av en enzymkatalysert reaksjon

Du studerer en enzymkatalysert reaksjon hvor enzymet katalyserer en reaksjon mellom et substrat og et produkt. Målingene viser følgende konsentrasjoner av substratet (\(S\)) over tid:

Tid (s)	Konsentrasjon (mM)
0	5.0
10	4.3
20	3.8
30	3.2
40	2.8
50	2.4
60	2.0

Lag en eksponentiell modell for nedbrytningen av substratet over tid.

Hypotesetesting

Hypotesetesting er en metode for å teste om en antagelse om en populasjon er sann. Vi har en nullhypotese \(H_0\) og en alternativ hypotese \(H_1\). Vi antar at nullhypotesen er sann, og ser hvor sannsynlig det er å observere dataene vi har gitt denne antagelsen. Hvis sannsynligheten er lav, forkaster vi nullhypotesen.

Uavhengig t-test

!pip install scipy

import numpy as np
from scipy.stats import ttest_ind, ttest_rel, ttest_1samp

pasienter_placebo = [129, 131, 135, 138, 130, 132, 137]
pasienter_medisin = [120, 125, 128, 121, 120, 119, 140]

t_verdi, p_verdi = ttest_ind(pasienter_medisin, pasienter_placebo)

alfa = 0.05

if p_verdi < alfa:
    print("Nullhypotesen kan forkastes. Forskjellen er signifikant.")
else:
    print("Forskjellen er ikke signifikant")

0.019426981050421992

Paret t-test

før_rens = [30, 45, 22, 50, 50]
etter_rens = [28, 33, 20, 40, 49]

t_verdi, p_verdi = ttest_rel(før_rens, etter_rens)
p_verdi

0.08003748732928705

T-test for ett utvalg

koffein = [200, 240, 222, 190, 212]
mu = 200

t_verdi, p_verdi = ttest_1samp(koffein, mu)
p_verdi

0.21456634958913234

Korrelasjon