Forelesning 8: Differensiallikninger og reaksjonskinetikk

import numpy as np
import matplotlib.pyplot as plt

# Startbetingelser
t0 = 0
y0 = 0
t_slutt = 100 # sekunder
dt = 1E-3

N = int((t_slutt - t0)/dt) + 1

# Arrayer
t = np.zeros(N)
y = np.zeros(N)

t[0] = t0
y[0] = y0

for i in range(N-1):
    # Differensiallikninga
    yder = 1
    # Eulers metode
    y[i+1] = y[i] + yder*dt
    t[i+1] = t[i] + dt    

plt.plot(t, y)
plt.show()

import numpy as np
import matplotlib.pyplot as plt

# Startbetingelser
t0 = 0
HI0 = 0
H20 = 1 # mol/L
I20 = 0.5 # mol/L
t_slutt = 500 # sekunder
dt = 1E-3
k = 0.1

N = int((t_slutt - t0)/dt) + 1

# Arrayer
t = np.zeros(N)
HI = np.zeros(N)
H2 = np.zeros(N)
I2 = np.zeros(N)

t[0] = t0
HI[0] = HI0
I2[0] = I20
H2[0] = H20

for i in range(N-1):
    # Differensiallikningene
    dHIdt = k*H2[i]*I2[i]
    dH2dt = -0.5*dHIdt
    dI2dt = dH2dt
    
    # Eulers metode
    #y[i+1] = y[i] + yder*dt
    HI[i+1] = HI[i] + dHIdt*dt
    H2[i+1] = H2[i] + dH2dt*dt
    I2[i+1] = I2[i] + dI2dt*dt
    # y_neste = y_forrige + difflikning*dt

    t[i+1] = t[i] + dt    

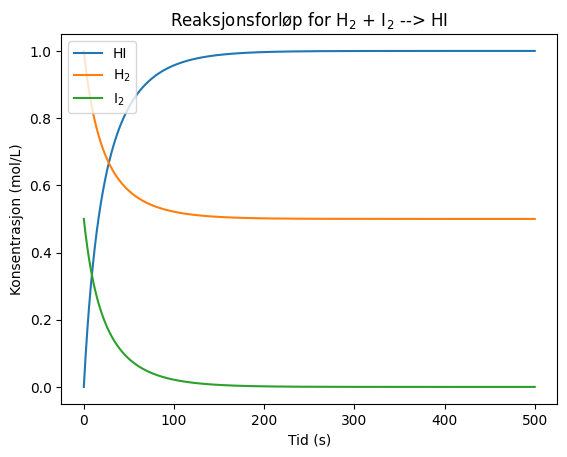
plt.plot(t, HI, label = "HI")
plt.plot(t, H2, label = "H$_2$")
plt.plot(t, I2, label = "I$_2$")
plt.xlabel("Tid (s)")
plt.ylabel("Konsentrasjon (mol/L)")
plt.title("Reaksjonsforløp for H$_2$ + I$_2$ --> HI")
plt.legend()
plt.show()