Forelesning 10: Molekylmekanikk

import numpy as np
import matplotlib.pyplot as plt

# Initialbetingelser
v0 = 0  # startfart (m/s)
s0 = 15 # startposisjon (m)
k = 100 # luftmotstandskoeffisient
m = 70  # masse (kg)
g = 9.8 # tyngdeakselerasjonen (m/s^2)

t0 = 0
t_slutt = 1.75
dt = 1E-4 
N = int((t_slutt - t0)/dt) + 1

# Arrayer
t = np.zeros(N)
v = np.zeros(N)
s = np.zeros(N)

t[0] = t0
v[0] = v0
s[0] = s0

# Integrasjonsløkke
for i in range(N - 1):
    F = - m*g - k*v[i] # Kreftene
    a = F/m            # Newtons 2. lov
    # Eulers metode
    v[i+1] = v[i] + a*dt
    s[i+1] = s[i] + v[i]*dt

    t[i+1] = t[i] + dt

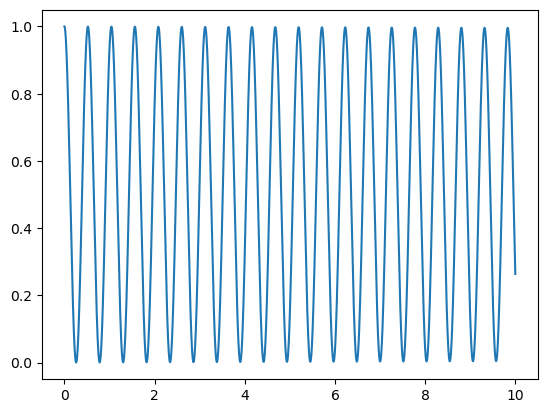
plt.plot(t,s)
plt.show()

# Annen tilnærming (programskisse)
s = 15
while s > 0:
    # Kjør løkka
    # ...
    s = s + v*dt

\[F = - k(T) \cdot (x - x_0)\]

\[k(T) = \alpha T(t)\]

\[T(t) = T_0 + \beta t\]

import numpy as np
import matplotlib.pyplot as plt

# Initialbetingelser
x0 = 1
v0 = 0
x_eq = 0.5
m = 1
T0 = 290
alpha = 0.5
beta = 1

t0 = 0
t_slutt = 10
dt = 1E-4
N = int((t_slutt - t0)/dt) + 1

def k(T, alpha):
    return alpha*T

def T(t, T0, beta):
    return T0 + beta*t

# Arrayer
x = np.zeros(N)
v = np.zeros(N)
t = np.zeros(N)

x[0] = x0
v[0] = v0
t[0] = t0

# Integrasjonsløkke
for i in range(N - 1):
    # Hookes lov
    F = -k(T(t[i], T0, beta), alpha)*(x[i] - x_eq)
    # Newtons 2. lov
    a = F/m
    # Euler-Chromers metode
    v[i+1] = v[i] + a*dt
    x[i+1] = x[i] + v[i+1]*dt

    t[i+1] = t[i] + dt

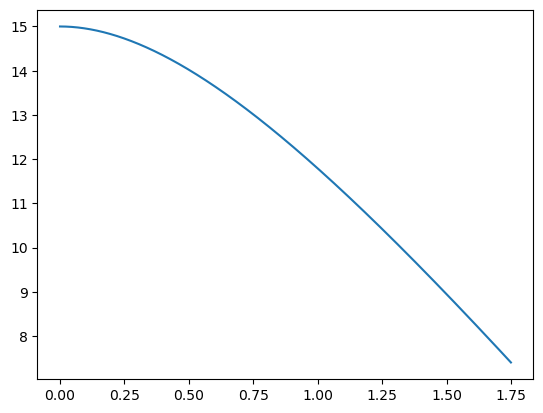
plt.plot(t, x)
plt.show()